Поля

Поля

Мы уже говорили, что понятие кольца, удовлетворяющего всем аксиомам (1), ока­залось в некоторых вопросах математики слиш­ком узким. Однако для других математических вопросов оно оказалось слишком широким, ведь в определении кольца ни звука не сказано о возможности деления. Да и не во всех коль­цах можно делить. Возьмем, например, кольцо всех (положительных и отрицательных) целых чисел. Если разделить 3 на 5, то целого числа не получится. А без деления нельзя решать даже уравнений первой степени!

Чтобы изучать уравнения, пришлось огра­ничиться кольцами, в которых есть операция деления. Такие кольца математики назвали полями. Как в настоящем поле можно идти в любую сторону, не встречая никаких пре­пятствий, так в математическом поле можно беспрепятственно выполнять все арифметичес­кие действия. Впрочем, одно ограничение есть — на нуль в поле делить нельзя.

Читатель еще в шестом классе познакомился с одним полем — полем всех рациональных чисел (положительных и отрицательных). Поз­же он познакомился с другим, более широким полем — всех действительных чисел (как ра­циональных, так и иррациональных). Наконец, все комплексные числа тоже образуют поле.

Кроме этих трех полей (рациональных, действительных, комплексных чисел), есть еще много других полей, состоящих из чисел. Возь­мем, например, все числа вида

где а и и b — рациональные числа. В это множество чисел входит, например

 но не входит


Покажем, что это множество чисел образует поле. В самом деле, возьмем два числа:

из нашего множества. Их сумма имеет вид:

Так как а+с и b+d — рациональные числа, то число


также принадле­жит нашему множеству. Точно так же из ра­венств: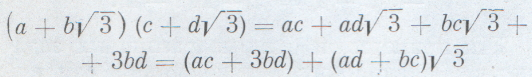



 следует, что произведение двух чисел рассмат­риваемого множества снова принадлежит ему. Сложнее обстоит дело с частным. Возьмем число

Чтобы записать его в виде m+

освободимся и от иррациональности в знаменателе: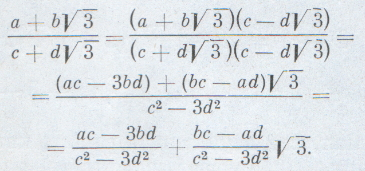






 

Числа



рациональны, а потому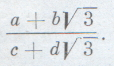



принадлежит нашему множеству. Впрочем, не спешите, не все числа можно делить друг на друга (даже в поле рациональ­ных чисел). Если число с²-3d² окажется рав­ным нулю, то у нас ничего не получится. Но при рациональных с т d равенство с²-3d²=0 может иметь место только в том случае, если с=d=0. А в этом случае число

равно нулю и делить на него нельзя.

Докажите сами, что числа

 где а и b — рациональны, образуют поле. А вот числа вида

где а, b, с— рациональны, не образуют поля, потому что

Что­бы получить поле, надо расширить это множество чисел, а именно рассматривать числа вида

где а, b, с, d — рацио­нальны. Поля можно строить не только из чи­сел. Например, множество всех алгебраичес­ких дробей образует поле.

 

• ЧЕМ ЗАНИМАЕТСЯ АЛГЕБРА

• ЧИСЛА И ДЕЙСТВИЯ
• Необычная конференция
• Фундамент алгебры 
• Сила букв 
• Кольца 
• Поля