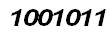Двоичная нумерация

Двоичная нумерация

В статье «Как люди считали в старину и как писали цифры» уже говорилось, что в двоич­ной системе нумерации обходятся двумя цифрами: нулем и единицей. Единица каждого следующего разряда числа в двоичной записи в два раза больше единицы предыдущего разряда: две «простые» единицы составляют двойку, две двойки — четверку, две четверки — восьмер­ку, две восьмерки — шестнадцать и т. д.

Число «один» записывается как обычно — «1». Но число «два» составляет уже единицу второго разряда и потому записывается так: «10» (одна двойка и нуль единиц). Число «три» изображается: «И» (одна двойка и одна едини­ца). Число «четыре» представляет собой еди­ницу третьего разряда и потому записывается «100» (одна четверка, нуль двоек и нуль еди­ниц). Дальнейшие числа в двоичной записи имеют вид:

пять — «101» (одна четверка, нуль двоек и одна единица),

шесть — «110» (одна четверка, одна двойка и нуль единиц),

семь — «111» (одна четверка, одна двойка и одна единица).

Восьмерка — это опять новый разряд — «1000» (нули указывают на отсутствие четве­рок, двоек и единиц). Далее идут:

девять — «1001» (одна восьмерка и одна единица),

десять — «1010» (одна восьмерка и одна двойка),

одиннадцать — «1011» (т. е. 8+2+1),

двенадцать — «1100» (т. е. 8+4),

тринадцать — «1101» (т. е. 8+ 4+1) и т. д.

Вот перед нами «загадочное» число:

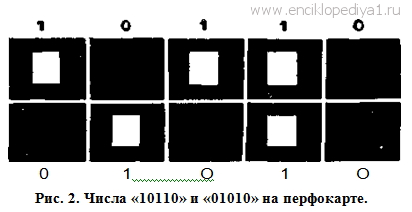
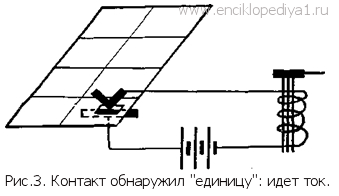
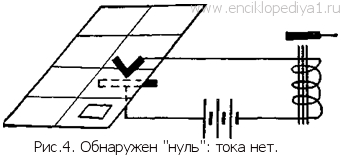
записанное в двоичной нумерации. Его легко «разгадать», подписав (справа налево) под каж­дым разрядом его значение:

      1        0       0         1      0    1       1

    (64)  (32)  (16)  (8)  (4)  (2)   (1).

Как видим, заинтересовавшее нас число скла­дывается из единицы, двойки, восьмерки и шес­тидесяти четырех (1+2+8 + 64). Очевидно, оно равно 75. Читатель, вероятно, теперь уже сам сможет определить, что двоичной записью 10110011 изображается число 179.

Одно из преимуществ двоичной записи — удобство изображения чисел разнообразными средствами и быстрой передачи их из одного места в другое. Например, пробитый квадратик особой картонной карточки (ее называют пер­фокартой) может изображать единицу, а це­лый — нуль (рис. 2). Поместив перфокарту между пружинящими контактами электриче­ской цепи (рис. 3), мы получим в ней ток, если в данном квадратике записана единица (кон­такты замкнутся через отверстие), и наоборот: если в данном квадратике записан нуль, тока в цепи не будет (рис. 4), так как кар­тонная прокладка изолирует контакты друг от друга.

Кратковременный электрический ток при­нято называть электрическим импульсом. Как видим, любое число, записанное по двоичной системе, легко может быть выражено после­довательностью электрических импульсов, при­чем наличие импульса в определенный момент времени означает единицу, а отсутствие его — нуль.

Впрочем, иногда предпочитают изоб­ражать нуль не отсутствием импульса, а им­пульсом тока, идущего в противоположном на­правлении (в этом случае не обязательно уже выдерживать строго определенные промежутки времени между импульсами). Продолжитель­ность импульса может быть очень малой, скажем, в 1 микросекунду (т. е. миллионную долю секунды), что дает возможность передать даже многозначное число почти мгновенно.

• МАТЕМАТИКА УЧИТ ПРЕДСКАЗЫВАТЬ И УПРАВЛЯТЬ
• Электронные вычислительные машины
• Создать электронный арифмометр!   
• Двоичная нумерация     
• Считают лампы  
• Обязанности вычислителя    
• Возможен ли такой автомат?  
• Главные части машины 
• Инструкция для машины   
• Исполнение программы     
• Программа с преобразованиями    
• Универсальность машины     
• Автоматический перевод                                      Странные результаты