Примеры конечных игр. Принцип минимакса

Примеры конечных игр. Принцип минимакса

Приведем несколько примеров конечных игр. Каждую из них мы запишем в нормаль­ной форме.

Пример 1. Рассматривается игра, ко­торую назовем «Поиск». В ней участвуют две стороны: К и С. К хочет найти С; С, наоборот, хочет спрятаться от К.

У С есть два места — убежища I и II, где он может прятаться. Выбирает он себе любое убежище. Игрок К по правилам игры тоже может искать С, где ему вздумается. Если он нашел С, С проиграл одно очко, если не нашел, т. е. пошел не в то убежище, где спрятался Г, то, наоборот, К проиграл одно очко. Тре­буется записать игру в нормальной форме.

Решение. У К — две стратегии:

К₁— искать в убежище I,

К₂— искать в убежище II.

У С — тоже две стратегии:

С₁ — прятаться в убежище I,

С₂ — прятаться в убежище II. Игра конечная — 2x2, матрица игры будет:

К этой игре мы еще вернемся в дальнейшем и найдем ее решение. А пока что просто порас­суждаем за игрока К. Представим себе, что мы игрок К и что нам предлагается выбрать себе стратегию. Что ж, попробуем! Выберем, на­пример, K₁, т. е. будем искать всегда в убе­жище I. Но тогда разумный противник через несколько партий догадается о нашей страте­гии и будет прятаться там, где мы его не ищем,

т. е. в убежище II. Плохо! Выберем стратегию К₂. Ничуть не лучше: противник снова дога­дается и будет прятаться в убежище I. Что же нам делать? Попробуем применять стратегии К₁ и K₂ попеременно, через одну партию игры. Но ведь противник и об этом может догадать­ся и будет прятаться каждый раз не там, где мы его ищем. Как ни кинь — все клин! Что же, значит, наше положение безвыходно? При лю­бом выборе стратегии нам придется проигры­вать? Выходит, что так.

Давайте теперь встанем на точку зрения противника. С удивлением мы обнаружим, что его положение — ничуть не лучше нашего! Какую бы стратегию он ни выбрал — все ему невыгодно.

Позже мы с вами решим эту игру, т. е. найдем пару оптимальных стратегий К и С. Впрочем, о них можно по секрету сообщить заранее: каждому игроку надо будет чере­довать свои стратегии, но не регулярно (че­рез одну), а случайным образом (например, подбросить монету и, если она упа­дет гербом, искать в убежище I, а если цифрой — в убежище II). Аналогично должен будет дей­ствовать и С. При этом в среднем на одну пар­тию будет приходиться нулевой выигрыш (цена этой игры будет равна нулю): К не будет ни выигрывать, ни проигрывать. Не очень при­ятно, но все-таки много лучше, чем всегда быть в проигрыше!

Здесь мы впервые столкнулись с одним из важных понятий теории игр — с понятием смешанной стратегии, т. е. чере­дования нескольких «чистых» стратегий по слу­чайному закону в определенных пропорциях, или, как говорят, с определенными часто­там и. В данном примере каждая из страте­гий применяется с частотой ¹/₂.

Рассмотрим теперь другую игру, решение которой уже не будет столь очевидным.

Пример 2. Игра «Три пальца».

Два игрока К и С одновременно и не сгова­риваясь показывают друг другу один, два или три пальца. Если всего показанных пальцев (первым и вторым вместе) будет четное число, то выигрывает К: он получает столько очков, сколько всего было пальцев, если нечетное — выигрывает С, на тех же условиях. Требуется записать игру в нормальной форме.

Решение. Перенумеруем стратегии по числу показанных пальцев. Игра 3x3. Матрица игры будет:

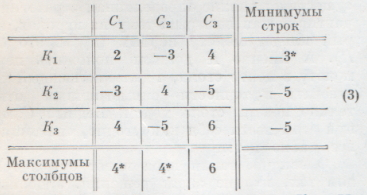
Поразмыслим немного над стратегиями каж­дой стороны. Станем сначала на сторону К. Предположим, что мы выбрали стратегию К₁. Что будет делать противник? Он разумен и хо­чет отдать поменьше. Ясно, он выберет страте­гию C₂; наш выигрыш при этом будет равен -3, т. е. мы потеряем 3 очка. Плоховато! За­пишем число -3 против первой строки в доба­вочном столбце (см. матрицу (3).

Попробуем другую стратегию — К₂. На нее разумный противник ответит С₃. Мы тогда потеряем 5 очков. Еще хуже! Третья страте­гия — К₃ — дает точно тот же результат: вы­игрыш (-5).

Что же делать? Пожалуй, лучше других будет все-таки стратегия К₁ — при ней мы по крайней мере не проиграем больше 3 очков! Ведь против этой стратегии стоит максималь­ное число дополнительного столбца — мы его отметили звездочкой.

Выбрав стратегию К₁, мы гарантируем себе, что, как бы ни вел себя противник, мы никак не проиграем больше 3 очков (т. е. не выиграем мень­ше (-3) очков). Величина (-3) есть макси­мальный гарантированный выигрыш, который мы («красные») можем себе обеспечить, приме­няя только одну-единственную стратегию. Та­кой стратегией должна быть К₁.

Как мы получили (-3)? Нашли минимум каждой строки и из этих минимумов взяли мак­симальный. Эта величина называется максимином или нижней ценой игры. Будем обозначать ее a.

Подумаем теперь за противника. Он тоже хочет отдать поменьше, а получить побольше. Но, какую бы он стратегию ни выбрал, мы («красные») поведем себя таким образом, чтобы получить с него побольше. Значит, противник («синие») должен в каждом столбце выписать не минимальное, а максимальное число (см. ниж­нюю добавочную строку в матрице (3).

Из этих максимумов он должен найти ми­нимальный, так называемый минимакс или верхняя цена игры, которую мы обозначим β. Эта величина в нашем случае равна 4 и отмечена звездочкой. Чтобы не проиграть больше 4, «синие» должны придерживаться любой из своих двух стратегий С₁, С₂.

Значит, если каждому участнику предлагается выбрать одну-единственную стратегию, то эти стратегии должны быть: К₁ для «крас­ных» и С₁ или C₂ для «синих».Как мы выбрали эти стратегии? Руководствуясь принципом осторожности, который говорит: в игре веди себя так, чтобы получить наибольшую выгоду при наихудших для тебя действиях противника. Этот принцип называется принципом минимакса и является в теории игр основным.

Применяя этот принцип, мы пока что реко­мендовали игроку К показывать один па­лец, игроку С — показывать один или два пальца.

Но нашли ли мы решение игры, т. е. та­кую пару стратегий, которая является равновесным положением? Легко убедиться, что нет. Найденные нами стратегии обладают досадным свойством: они неустойчивы. Действительно, пусть оба игрока дер­жатся рекомендованных чистых стратегий: К₁ и, скажем, С₁. Пока оба держатся этих стратегий, выигрыш будет равен 2, т. е. на каж­дую партию игры С проигрывает К два очка. К, может быть, и доволен, но С досадно. Он не хочет проигрывать. Допустим, он откуда-то узнал, что мы придерживаемся стратегии К₁. Что он будет делать? Разумеется, немедленно перейдет к стратегии С₂ и будет получать по 3 очка, т. е. сведет наш выигрыш к -3. А если мы теперь узнаем о поведении С? Перейдем на стратегию К₂. В ответ на это С переидет на С₃ и т. д.

Мы убедились, что пара стратегий, выте­кающих из принципа минимакса, неустой­чива: стоит одному игроку узнать, что делает другой, как равновесие нарушается...

Всегда ли это будет так? Оказывается, не всегда.

• ТЕОРИЯ ИГР

• Чем занимается теория игр    
• Парная игра с нулевой суммой. Цена игры      
• Игра в нормальной форме. Матрица игры    
• Примеры конечных игр. Принцип минимакса    
• Седловая точка. Чистая цена игры    
• Решение игры в смешанных стратегиях. Основная теорема теории игр