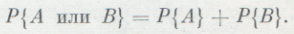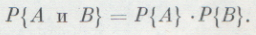Теоремы сложения и умножения вероятностей

Теоремы сложения и умножения вероятностей

Прежде всего рассмотрим две важные фор­мулы, которые лежат в основе действий с ве­роятностями. Эти формулы носят название теорем сложения и умножения вероятностей. Пусть два события А и В таковы, что при каждом испытании может появиться только одно из них или же ни одного, а вместе появить­ся они не могут. Такие события называются несовместными. Теорема сложения утверждает, что если А и В несовместны, то

Представим теперь себе, что события А и В таковы, что наступление одного из них не из­меняет вероятности наступления другого. Та­кие события называются независимыми. Для независимых событий имеет место теорема умножения, состоящая в следующем:

Рассмотрим для иллюстрации следующую задачу, с которой в настоящее время прихо­дится часто встречаться при организации про­изводства. Ремонтный рабочий обслуживает 6 механизмов, каждый из которых независимо от других может выйти из нормального рабо­чего режима и потребовать к себе внимания. Вероятность выхода каждого из механизмов за период длительности Т равна р. Чему равна вероятность того, что за период длительности Т из рабочего режима выйдет не более чем 2 механизма? Вероятность того, что данный механизм за весь период работы не выйдет из нормального рабочего состояния, равна 1 — р. По теореме умножения вероятность того, что все шесть механизмов проработают благополучно, равна (1-р)⁶ Вероятность того, что определенный меха­низм выйдет из нормального состояния работы, а остальные пять будут работать хорошо, рав­на по теореме умножения р(1-р)⁵. Меха­низмом, потребовавшим внимания, может ока­заться любой из 6, поэтому вероятность того, что из строя выйдет только один механизм (без­различно какой), равна по теореме сложения

6p(1-p)⁵.

Вычислим еще вероятность того, что какие-то два механизма выйдут из рабочего состоя­ния, а остальные четыре будут работать нор­мально. С этой целью заметим, что по теореме умножения вероятность выхода из строя двух определенных механизмов и нормальной рабо­ты остальных четырех равна р²(1-р)⁴. Но два механизма из шести можно выбрать C²₆= 15 различными способами. Для каж­дого из них вероятность уже вычислена. В результате по теореме сложения искомая ве­роятность равна 15р²(1-р)⁴.

Так как интересующее нас событие (выход из нормального рабочего состояния не более чем двух механизмов) может осуществиться следующими несовместимыми способами: все механизмы будут работать безотказно, отка­жет лишь один механизм, откажут в точности два механизма, то его вероятность по теореме сложения равна:

(1-р)⁶+6р(1-р)⁵+15р²(1-р)⁴.

Если, для примера, вероятность выхода ме­ханизма из нормального рабочего состояния равна 0,2, то вероятность того, что за указан­ный срок:

все механизмы будут работать нормально, равна 0,262144;

только один механизм выйдет из строя, равна 0,393216;

только два механизма выйдут из строя, равна 0,245760.

Таким образом, при указанных условиях работы искомая вероятность равна 0,90112.

• НАУКА О СЛУЧАЙНОМ
• Обыденные представления     
• Примеры случайных событий
• Зачем нужно изучать случайные явления     
• Зарождение науки о случае    
• Теоремы сложения и умножения вероятностей     
• Дополнительные исторические сведения        
• Закон больших чисел                                                        Сколько рыб в озере?
• Некоторые современные направления развития теории вероятностей