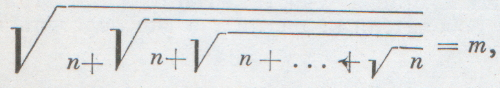Математические олимпиады IX класс

Математические олимпиады IX класс

1. В клетки таблицы nXn (n — нечетное) произ­вольным образом вписаны числа так, что в каждой клет­ке стоит число, равное +1 или -1. Произведение чисел, стоящих в каждой строке, обозначим через a_k, а произведение чисел, стоящих в каждом столбце,— через b_k (k=1, 2,..., n). Доказать, что

a₁+a₂+...+а_n+b₁+b₂+...+b_n≠0.

2. Решить в целых числах уравнение

где

3. На плоскости нарисована сеть, образованная из правильных шестиугольников со стороной 1. Жук прополз, двигаясь по линиям сети, из узла А в узел В по кратчайшему пути, равному 100. Доказать, что поло­вину всего пути он полз в одном направлении.

X-XI классы